Answering some 'Forecasting with GAMs in R' questions
After running the 'Forecasting with generalised additive models (GAMS) in R' workshop with Forecasting for Social Good, there were a few questions that we didn't get the chance to answer. This blog post aims to answer some of them.
February 26, 2024
Last week I had the pleasure of running the Forecasting with generalised additive models (GAMS) in R workshop organised by Forecasting for Social Good. During the workshop, we covered what GAMs are and why we might want to use them, fitting GAMs in R with {mgcv}, evaluating models, making forecasts, and some of the reasons that GAMs might not work. The workshop materials can be found online:
- Slides: nrennie.github.io/f4sg-gams
- GitHub: github.com/nrennie/f4sg-gams
There were a few questions that we didn’t get the chance to answer. And in some cases, now that I’ve had a bit more time to think, I have better answers for some of the questions I did answer! So I’ve shared those answers here instead.
Questions
Smoothing in GAMs
What’s the difference between the sp and k parameters?
The k argument sets up the dimensionality of the smoothing matrix for each term. It is set within the s() function, and the default value is 10. Read the ?choose.k help files for some guidance on choosing k - notably the guidance states that “exact choice of k is not generally critical: it should be chosen to be large enough that you are reasonably sure of having enough degrees of freedom to represent the underlying ‘truth’ reasonably well, but small enough to maintain reasonable computational efficiency.”. In the workshop, we also looked at using gam.check() which can help to flag up terms for which k is too low.
The sp argument is a smoothing parameter. It can be set either in the gam() function for all terms or in the s() function for each individual term. If you don’t explicitly set a value for sp, it is automatically calculated. You can set the method used to calculate is using the method argument. You can alternatively specify min.sp - a lower bound(s) for the smoothing parameter(s).
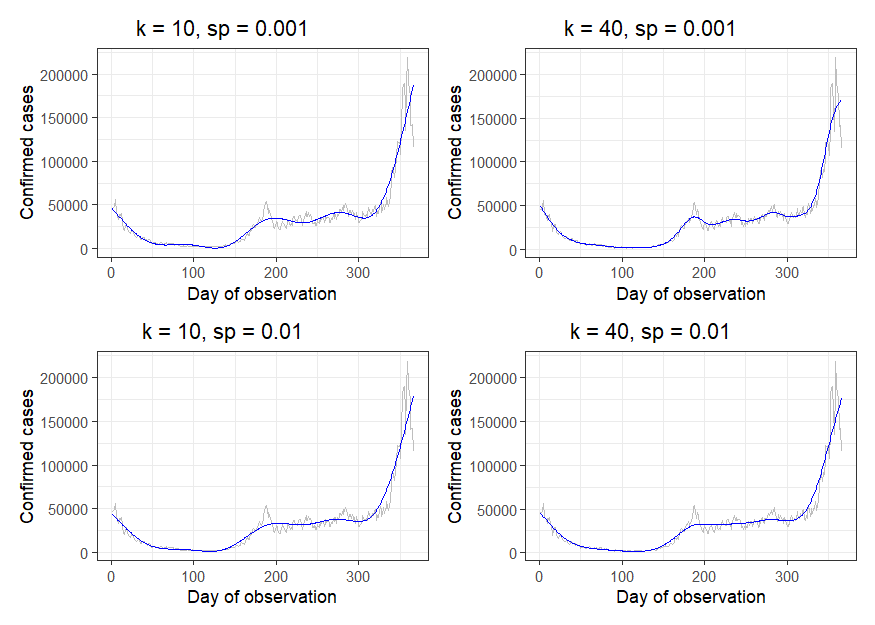
How do we choose the value of sp?
If you don’t explicitly set a value for sp, it is automatically calculated. The gam() function attempts to find the appropriate smoothness for each model term using prediction error criteria or likelihood based methods. You can choose which method is used to select the smoothing term by using the method argument of s() - read ?gam.selection for some further discussion on which method might be best for your data. My preference is REML (restricted maximum likelihood) - it’s less prone to local minima than the other methods.
Can we do regularisation do avoid over-fitting?
Yes, you can modify the smoothing penalty to include an additional shrinkage term. Setting the bs argument in s() to either "cs" or "ts" gives a smoothness penalty with a shrinkage component. For large enough smoothing parameters the smooth becomes identically zero which means the term is effectively removed from the model.
What different types of basis functions are available?
The {mgcv} package has several types of smooth classes built-in, and you can also add your own if you wish (see ?user.defined.smooth). You can use thin plate regression splines (the default), Duchon splines, cubic regression splines, splines on the sphere, B-splines, P-splines, random effects, Markov random fields, Gaussian process smooths, or soap film smooths. See ?smooth.terms for a full list and details of argument names.
Modelling
Is the gam function compatible with the {tidymodels} framework?
Yes! The gen_additive_model() function in the {parsnip} package allows you to fit GAMs in {tidymodels} - and they are fitted with the {mgcv} package. You can read the help files here:
parsnip.tidymodels.org/reference/gen_additive_mod.html
Can we include interaction terms in a GAM?
Yes, there are two ways to include interaction terms in GAMs in {mgcv}, depending on whether you want one or both of the terms are smoothed variables:
- For an interaction between two smoothed variables
xandy, adds(x, y)(for e.g. spatial coordinates) orte(x, y)orti(x, y)to the right hand side of the formula ingam(). - For an interaction between a smoothed variable
x, and a linear variabley, adds(x, by = y)(orte()orti()) to the right hand side of the formula ingam(). Here,ycan be either continuous (then the linear effect ofyvaries smoothly withx) or a factor (where it should also be a main effect and you’ll have a smooth term that varies between different levels ofy).
Can we use AIC to select models?
Yes, you can use the AIC value to compare and select between models. You can also use other criteria such as the generalised cross validation scores for similar comparisons. Run ?gam.selection to see a more in-depth discussion of model selection, including choosing parameters.
How do we do variable selection for GAMs?
You can also look at the (approximate) p-values in the output of summary() to identify which terms might be removed from the model. However, I’d caution against using step-selection procedures for models (not just GAMs) - it tends not to be particularly successful. It’s better to start by thinking about what an appropriate model might be based on domain knowledge, and compare variations of models from that starting point. There’s some further discussion of this point in the documentation - try running ?gam.selection to read it.
Forecasting
Can we get confidence intervals?
When creating predictions using GAMs with the predict function, we can also return standard error estimates for each prediction.
| |
The {gratia} package allows you to calculate confidence intervals for smoothed fits more easily:
| |
Can we detect outliers using GAMs?
You can start by inspecting the residuals from your fitted GAM. However, detecting outliers using GAMs is tricky - it will highly depend on the smoothness of the fit. If you choose a high dimensional basis and/or a low level of smoothing, the GAM will fit the observed data closely - meaning few observed points are far away from the fitted values, and there are few, if any, outliers. Similarly, a low dimensional basis or high level of smoothing will result in more outliers.
Sometimes we also need to forecast regressors, in order to make our primary forecasts. Can we also forecast regressors in a single GAM fit?
Let’s say in our Covid data example from the workshop, we’ve fitted a GAM with smooth terms for day and number of tests to predict confirmed cases. We know we want to make a prediction for day 370 but we don’t know how may tests will be performed that day, so first we need to predict the number of tests.
| |
After we’ve fitted our model, we have a smooth fit for tests, but this doesn’t depend on date_obs so we can’t make a prediction for tests based on date_obs from this model. I think, we’d need to fit a model that has tests as an outcome, and date_obs as a predictor. As far as I can tell, there’s no easy way to do this automatically. Including missing regressors or NA values in newdata argument of the predict() function results in errors, NA values being returned, or rows being dropped.
Additional resources
Any of the following resources are fantastic next steps in your journey with GAMs in R:
GAMs resource list: github.com/noamross/gam-resources
{mgcv} course: noamross.github.io/gams-in-r-course
GAMMs: r.qcbs.ca/workshop08/book-en/introduction-to-generalized-additive-mixed-models-gamms.html
DGAMs for forecasting: doi.org/10.1111/2041-210X.13974 and the {mvgam} R package.
Ecological forecasting with GAMs Physalia workshop: github.com/nicholasjclark/physalia-forecasting-course
I’m hoping this has answered most of the remaining questions!

Image: giphy.com
For attribution, please cite this work as:
Answering some 'Forecasting with GAMs in R' questions.
Nicola Rennie. February 26, 2024.
nrennie.rbind.io/blog/forecasting-gams-r-questions
BibLaTeX Citation
@online{rennie2024,
author = {Nicola Rennie},
title = {Answering some 'Forecasting with GAMs in R' questions},
date = {2024-02-26},
url = {https://nrennie.rbind.io/blog/forecasting-gams-r-questions}
}
Licence: creativecommons.org/licenses/by/4.0